摘要: 结合连续挤压工艺制定 Gleeble －1500 热压缩试验方案，测定 H62 黄铜合金流变应力，采用 Arrhenius 方程的指数形式描述 H62 黄铜的本构关系，绘制 H62 黄铜合金的热加工图，预测 H62 黄铜合金在连续挤压过程中的功率耗散因子 η 和组织的分布，以及塑性失稳区的位置，确定 H62 黄铜合金的***佳热变形参数为应变速率为 0.01s－ 1，温度为 400 ～ 500℃ 。

关键词: 金属材料; 黄铜合金; 连续挤压; 热加工图; 本构关系; 流变应力

中图分类号: TG146 11; TG113 25 文献标识码: A 文章编号: 1001 －0211( 2010) 02 －0007

金属热变形流变应力是材料在高温下的基本性能之一，它不仅受变形温度、变形程度、应变速率和合金化学成分的影响，也是变形体内部显微组织演变的综合反映。无论在制定合理的热加工工艺方面，还是在以塑性有限元为代表的现代塑性加工力学中，其精确的流变应力数值或表达式是提高理论计算精度的关键。为此，国内外近些年来在这方面的研究十分活跃。

然而对于 H62 黄铜合金流变应力的研究报道甚少。采用 Gleeble － 1500 热模拟机，结合连续挤压工艺，制定工艺方案。在变形温度为 100 ～ 800℃ 和应变速率为 0.01 ～ 1s－ 1的变形条件下，对 H62 黄铜合金进行了等温热压缩实验，通过对黄铜合金热压缩变形流变应力与变形程度、应变速率以及变形温度之间的关系分析，建立本构方程及热加工图，为合理制定黄铜合金热变形工艺提供参考，以及为有限元数值模拟进一步分析提供准确数据或数学模型。

1.流变应力曲线分析

连续挤压过程中挤压轮转速一般为 6r/min ～10r / min，在 1s－ 1数量级上，所以结合连续挤压工艺，分析其应变速率为 1s－ 1的流变应力曲线如图 1 所示。

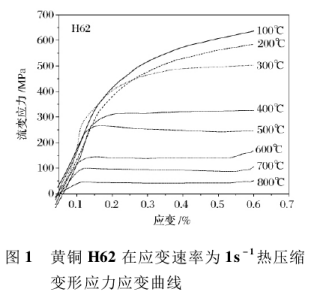
结果表明，H62黄铜在400℃ 以上、流变应力出现了波峰，而后又呈直线。从图 1 还可以看出，峰值应力对应的应变随温度的升高而不断减小。真应力－ 真应变曲线大致可以分为三个阶段。***阶段变形量较小时，随着应变的逐步增加，位错密度也增加，位错消失速度也随之增大。反映在真应力真应变曲线上是随着变形量加大，加工硬化速度减弱，但是在***阶段总的趋向还是加工硬化超过动态软化，因此随着变形量的增加，变形应力还是不断增加的。第二阶段当应变量超过一定值后，应力下降，表明材料在该温度下已经发生了动态再结晶，动态再结晶的发生与发展使更多的位错消失，材料的变形应力很快下降。第三阶段，应变达到一定的时候，应力与应变呈现出稳态流变的特征，由于流变应力在此条件维持一稳定值，加工硬化和动态再结晶软化达到平衡［3］。

变形温度保持不变时，应变速率越低，稳态变形阶段的流变应力也越低。从图 2 可以看出，温度和应变速率是影响流变应力的重要因素。在同一温度下，材料的应力峰值随应变速率的增大而增大。一般认为，较低时材料中的储存能较高，从而有利于材料在热变形过程中发生动态再结晶［4］。在较高的应变速率下，塑性变形时单位应变的变形时间缩短，能发生运动的位错的数目增加。同时由于动态回复、动态再结晶等提供的软化过程时间缩短，塑性变形不充分，导致流变应力的增大。在同一应变速率下，温度越高，原子的热激活能的作用越大，原子振动加强，原子间的临界切应力减弱，此外动态回复、动态再结晶引起的软化程度也随着温度的升高而增大，从而导致应力峰值的降低［5］，而且随着温度升高，变形速率越小，动态再结晶的临界应变值 ε 变小，即表示材料在高温下动态再结晶很快发生［6］。

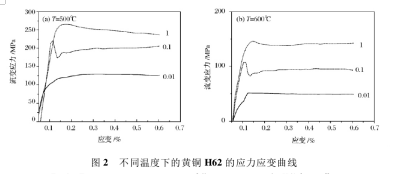
2.本构方程

H62黄铜合金在变形过程中对变形温度和应变速率都很敏感，研究表明［7］，z 与 σ 之间服从关系式( 1) ，式中: z 为 Zener-Hollomon 参数，z = ε′·exp( Q/RT) ; A 和 а 为材料常数或应变的函数; Q 为变形激活能，k·J·mol－ 1; σ 为流动应力，MPa; ε′为应变速

率，s－ 1。式 ( 1) 可以表示为 z = A′σn 和 z = Aexp( βσ) ，由 Zener-Hollomon 参数的定义，ε′可分别表示为式( 2) ～ 式( 4) 。

z = A1［sinh( аσ) ］n( 1)

ε′ = A1［sinh( аσ) ］nexp( -Q / RT) ( 2)

ε′ = g Ag′σnexp( -Q / RT) ( 3)

ε′ = Aexp( βσ) exp( -Q / RT) ( 4)

在回归 H62 合金本构方程时，首先分别以 lnσ和 lnε′及 σ 和 ln( ′为坐标作图，再用***小二乘法线性回归，依据式( 3) 和式( 4) ，分别对两式两边取对数，再将 H62 合金的热压缩试验数据代入可以得到lnε′-lnσ 图及 lnε′-σ 图的斜率，分别近似表示 n 和β。再将 а 和 n 的值代入式( 5) ，式( 5) 由式( 2) 两边取对 数 而 得，得 到 该 合 金 的变 形 激 活 能 Q =214 644k J / mol，代入 Zener-Hollomon 参数得式( 6 ) 。再将不同变形温度下 H62 黄铜合金热变形时的应变速率代入( 6) 式得到不同的 z 值，再与对应的峰值应力一起代入式( 7) 、式( 8) 和式( 9) ，用***小二乘法线性回归，得到 lnz-ln［sinh( аσ) ］关系、lnz-lnσ 关系和 lnz-σ 关系的相关系数分别为 0.98148，0.98421和 0.96619，另外将所得到的 n 和 β 值与前面所获得的 n 和 β 值相比较，结果表明 z 参数的对数和峰值应力关系较好地满足线性关系，即 H62 黄铜合金高温变形时的流变应力方程遵从Zener-Hollomon 参数的指数函数形式，从而 H62 黄铜合金高温变形时的应变速率 ε′，流变应力 σ 和温度 T 之间的关系可用式( 3) 描述［8］，则热激活能 Q 由式( 10) 求得。

Q = R{ γln［sinh( аσ) ］/ ( 1 / T) }ε′·{ ln( ′ / ln［sinh( аσ) ］}T( 5)

z = ε′·exp( 214 644 / RT) ( 6)

lnz = ln A′ + nln［sinh( аσ) ］ ( 7)

lnz = ln A′ + nlnσ ( 8)

lnz = ln A′ + βσ ( 9)

Q = ［lnσ / ( 1 / T) ］ε′·［lnε′ / lnσ］T·R( 10)

将求得的 A，n 和 Q 等材料参数值代入( 3) 式，得 H62 黄铜合金热压缩变形时的流变应力方程式( 11) 。

ε′ = e－ 9 7σ7 95exp( － 215517 / RT) ( 11)

3.热加工图理论

动态材料模型认为材料的热变形过程是一个能量耗散系统。外界输入的能量 p( 公式( 12) ) 可分为两部分，即耗散量( G) 和耗散协量( J) 。其中耗散量 G 为材料发生塑性变形所耗散的能量，绝大部分转化为热能，小部分以晶体缺陷的形式储存，而耗散协量 J 为材料在变形过程中发生组织演变所耗散的能量［9］。在一定的应变和温度条件下，这两种能量变化 的 比 值 为 应 变 速 率 敏 感 因 子 m，见 公 式( 13)［10］。

p = σε′ = G + J = ∫ σ·d( ′ + ( ε′·dσ ( 12)

m = d J / d G = ［( logσ) / ( logε′) ］ε，T ( 13)

当 m = 1 时，材料的热变形过程为理想线性耗散系统，耗散协量 J 取***大值( Jmax= σε′ /2 ) 。功率耗散因子 η( η = J /Jmax) 为材料在变形过程中组织演变所耗散的能量与理想线性耗散能量的比值［11］，表达式为式( 14) 和式( 15) 。

η = ( p-G) / Jmax= 2-2G / ( σε′) ( 14)

G = ∫ σ · dε′ ( ε′ = 0 ～ ε′min) + ( σ·dε′( ε′ =ε′min～ ε′) = ［

σε′ / ( m + 1) ］ε′ = ε′min+ ( σ·dε′( ε′= ε′min～ ε′) ( 15)

一般 物 理 模 拟 实 验 中 应 变 速 率 通 常 ε′ ≥0.001s－ 1，因此可取 ε′ = 0001s－ 1。当材料的本构关系满足 σ = Kε′时，功率耗散因子 η 可表达为公式( 16) 。功率耗散因子 η 随变形温度和应变速率的变化构成了功率耗散图。由于塑性成形过程中各种损伤过程和冶金变化过程都要耗散能量，因此借助金相观察和功率耗散图可以分析不同区域的变形机理［9 － 11］。

η = J / Jmax= 2m / ( m + 1) ( 16)

Prasad 失稳判断准则的描述如式 ( 17 ) 所示。H62 黄铜合金在 5 种温度及 3 种应变速率下，真应变为 0.5 时应力值列于表 l。表 l 数据显示，采用 3次样条函数拟合流变应力 logσ 与 logε′的函数关系，根据公式( 13) 计算出应变速率敏感指数 m，再用公式 ( 16) 计算可得出耗散效率因子 η。利用Matlab软件在由 T 和 logε′所构成的平面内绘制出等功率耗散效率因子 η 的轮廓曲线再按照式( 17) 给出的在加工图中流变失稳的判据标准，可以得出在不同变形温度下 ξ( ε) 的区域，该区域内变形将出现流变失稳［12 － 14］。H62黄铜合金的热加工图见图 3。

ξ( ε′) = log［m / ( m + 1) ］/ ( logε′) + m < 0( 17)

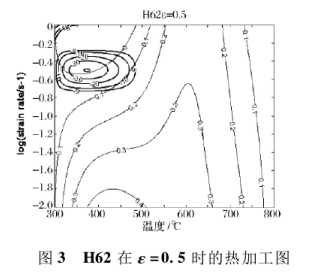
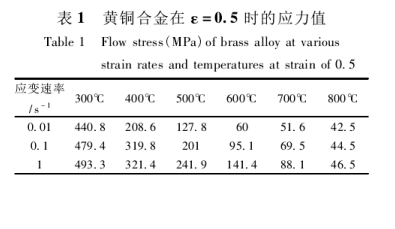
由图 3 可以看出，变形温度及应变速率不同，合金的动态能量消耗行为明显不同。随着变形温度的升高及应变速率的降低，η 值明显增加，即合金的动态能 量 消 耗 能 力 增 强，H62 在 变 形 温 度 400 ～500℃ 、应变速率为 0. 01s－ 1时，能量耗散因子达到峰值，约为 40% 。在 350 ～ 650℃能量耗散因子出现一个等高平台，约为 30% 。根据曲线观察这个区域可能是发生动态再结晶的区域，此时的动态再结晶软化作用有利于合金的均匀性变形。在这个区域进行热加工，能够得到无缺陷和优异的力学性能［15］。其典型温度的金相组织如图 4 所示，根据组织观察的结果可以确定出热加工中的完全再结晶区 400 600℃ 。

图 3 中粗实线为流变失稳图中级数( Level) 为负值的区域，为根据Prasad 失稳准则计算得到的流变失稳区，在失稳图中，当失稳判据为负数时，表示该区域流变不稳定。

当这个负的失稳判据绝对值越大时，表示流变不稳定的可能性越大。为了安全起见，制定热加工工艺时，应该避免失稳区域［10］。可以看出 H62 合金在低于 500℃ 应变速率为0.1 ～ 1 区域发生流变失稳，根据组织观察会容易发生晶界开裂［16］，制定热加工参数时应避免这些加工条件，由 H62 的热加工图可知，H62 合金在 400 ～500℃ ，应变速率为 0.0 01s－ 1时，耗散因子值***大，比较适宜在此条件下进行热加工。

4.结论

用 Arrhenius 方程的指数 形 式 能较 好 的 描 述H62黄铜合金高温变形时的流变应力行为。用热加工图理论分析材料的高温变形行为能准确直观地反映出材料在不同变形条件下的组织演变规律。结合曲线、金相组织观察得出 H62***佳热变形参数为应变速率为 0. 01s－ 1，变形温度为 400 ～ 500℃。

来源：中国知网   作者：王延辉